Arc Length

The length of the path \({\bf c}(t)=(x(t),y(t),z(t))\) for \(t_0\leq t\leq t_1\), is \[ L({\bf c})=\int^{t_1}_{t_0}\sqrt{[x'(t)]^2+[y'(t)]^2+[z'(t)]^2}\,{\it dt}. \]

example 1

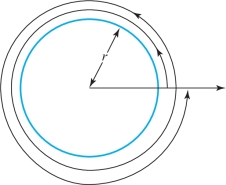
The arc length of the path \({\bf c}(t)=(r\,\cos t,r \,\sin t)\), for \(t\) lying in the interval \([0, 2\pi]\); that is, for \(0\leq t\leq 2\pi\), is \[ L({\bf c})=\int^{2\pi}_0\sqrt{(-r\,\sin t)^2+(r\,\cos t)^2}\, {\it dt}=2\pi r, \] which is the circumference of a circle of radius \(r\). If we had allowed \(0\leq t\leq 4\pi\), we would have obtained \(4\pi r\), because the path traverses the same circle twice (Figure 4.13).

Figure 4.13: The arc length of a circle traversed twice is 4\(\pi r.\)

example 2

Consider the point with position function \[ {\bf c}(t)=(t-\,\sin t,1-\,\cos t), \] which traces out the cycloid discussed in Section 2.4 (see Figure 2.4.6). Find the velocity, the speed, and the length of one arch.

solution The velocity vector is \({\bf c}'(t)=(1-\,\cos t,\,\sin t)\), so the speed of the point \({\bf c}(t)\) is \[ \|{\bf c}'(t)\|={\sqrt{(1-\,\cos t)^2+\,\sin^2t}}=\sqrt{2-2\,\cos t}. \]

Hence, \({\bf c}(t)\) moves at variable speed although the circle rolls at constant speed. Furthermore, the speed of \({\bf c}(t)\) is zero when \(t\) is an integral multiple of \(2\pi\). At these values of \(t\), the \(y\) coordinate of the point \({\bf c}(t)\) is zero, and so the point lies on the \(x\) axis. The arc length of one cycle is \begin{eqnarray*} L({\bf c}) &=& \int^{2\pi}_0\sqrt{2-2\,\cos t}\,{\it dt}=2\int^{2\pi}_0\sqrt{\frac{1-\,\cos t}{2}}\,{\it dt}\\[6pt] &=& 2\int^{2\pi}_0\,\sin \frac{t}{2}\,{\it dt}\,\bigg(\hbox{because } 1-\,\cos t=2\,\sin^2 \frac{t}{2} \hbox{ and }\sin \frac{t}{2}\geq 0 \hbox{ on } [0,2\pi]\bigg)\\[6pt] &=& 4\bigg(-\cos \frac{t}{2}\bigg)\bigg|^{2\pi}_{0}=8.\\[-27pt] \end{eqnarray*}

example 3

A billiard ball on a pool table follows the path \({\bf c}\colon\, [-1,1]\rightarrow {\mathbb R}^2\), defined by \({\bf c}(t)=(x(t),y(t),z(t))= (|t|, |t-\frac{1}{2}|)\). Find the distance traveled by the ball.

solution This path is not smooth, because \(x(t)=|t|\) is not differentiable at 0, nor is \(y(t)= |t-\frac{1}{2} |\) differentiable at \(\frac{1}{2}\). However, if we divide the interval \([-1,1]\) into the pieces \([-1,0],[0,\frac{1}{2}]\), and \([\frac{1}{2},1 ]\), we see that \(x(t)\) and \(y(t)\) have continuous derivatives on each of the intervals \([-1,0], [0,\frac{1}{2} ]\), and \([\frac{1}{2},1]\). (See Figure 4.14.)

Figure 4.14: A piecewise smooth path.

On \([-1,0],x(t)=-t,y(t)=-t+\frac{1}{2}\), so \(\|{\bf c}'(t)\|=\sqrt{2}\). Hence, the arc length of \({\bf c}\) between \(-1\) and 0 is \(\int^0_{-1}\sqrt{2}\,{\it dt}=\sqrt{2}\). Similarly, on \( [0,\frac{1}{2} ],x(t)=t, y(t)=-t+\frac{1}{2}\), and again \(\|{\bf c}'(t)\|=\sqrt{2}\), so that the arc length of \({\bf c}\) between 0 and \(\frac{1}{2}\) is \(\frac{1}{2}\sqrt{2}\). Finally, on \([\frac{1}{2},1]\) we have \(x(t)=t,y(t)=t-\frac{1}{2},\) and the arc length of \({\bf c}\) between \(\frac{1}{2}\) and 1 is \(\frac{1}{2}\sqrt{2}\). Thus, the total arc length of \({\bf c}\) is \(2\sqrt{2}\). Of course, we can also compute the answer as the sum of the distances from \({\bf c}(-1)\, {\rm to}\, {\bf c}(0) \,{\rm to}\, {\bf c}(\frac{1}{2})\) to \({\bf c}(1)\).

example 4

Find the arc length of \((\cos t,\,\sin t, t^2),0\leq t\leq \pi\).

solution The path \({\bf c}(t)=(\cos t,\,\sin t,t^2)\) has the velocity vector given by \({\bf v}=({-}{\sin t}, \,\cos t,2t)\). Because \[ \|{\bf v}\|=\sqrt{\,\sin^2 t+\,\cos^2 t+4t^2}=\sqrt{1+4t^2}=2\sqrt{t^2+\Big( \frac{1}{2}\Big)^2}, \] the arc length is \[ L({\bf c})=\int^\pi_02\sqrt{t^2+\bigg(\frac{1}{2}\bigg)^2}\,{\it dt}. \]

This integral may be evaluated using the following formula from the table of integrals: \[ \int \sqrt{x^2+a^2}{\,d} x=\frac{1}{2} \big[ x\sqrt{x^2+a^2}+a^2\,\log\, (x+\sqrt{x^2+a^2}) \big]+C. \]

Thus, \begin{eqnarray*} L({\bf c}) &=& 2\,{\bf \cdot}\, \frac{1}{2}\left[ t\sqrt{t^2+\bigg(\frac{1}{2}\bigg)^2}+ \bigg(\frac{1}{2}\bigg)^2 \log\left(t+\sqrt{t^2+\bigg(\frac{1}{2}\bigg)^2}\right)\right] \Bigg|^\pi_{t=0}\\[4pt] &=&\pi\sqrt{\pi^2+\frac{1}{4}}+\frac{1}{4}\log \bigg(\pi+\sqrt{\pi^2+\frac{1}{4}}\bigg)-\frac{1}{4} \log\bigg(\sqrt{\frac{1}{4}}\bigg)\\[4pt] &=&\frac{\pi}{2}\sqrt{1+4\pi^2}+\frac{1}{4}\log\, (2\pi+ \sqrt{1+4\pi^2})\approx10.63. \\[-16pt] \end{eqnarray*}

As a check on our answer, we may note that the path \({\bf c}\) connects the points (1, 0, 0) and \((-1,0,\pi^2)\). The distance between these points is \(\sqrt{4+\pi^2}\approx 3.72\), which is less than 10.63, as it should be.

Arc-Length Differential

An infinitesimal displacement of a particle following a path \({\bf c}(t)=x(t){\bf i}+y(t){\bf j}+z(t){\bf k}\,\) is \[ d{\bf s}={\it dx}\, {\bf i}+{\it dy}\, {\bf j}+{\it dz}\, {\bf k}=\bigg(\frac{{\it dx}}{{\it dt}}{\bf i}+\frac{{\it dy}}{{\it dt}}{\bf j}+\frac{{\it dz}}{{\it dt}}{\bf k}\bigg)\,{\it dt}, \] and its length \[ ds={\textstyle\sqrt{{\it dx}^2+{\it dy}^2+{\it dz}^2}}=\sqrt{\bigg(\frac{{\it dx}}{{\it dt}}\bigg)^2+ \bigg(\frac{{\it dy}}{{\it dt}}\bigg)^2+\bigg(\frac{{\it dz}}{{\it dt}}\bigg)^2}\,{\it dt} \] is the differential of arc length. See Figure 4.15.

Arc Length in \({\mathbb R}^n\)

Let \({\bf c}\colon\, [t_0,t_1]\rightarrow {\mathbb R}^n\) be a piecewise \(C^1\) path. Its length is defined to be \[ L({\bf c})=\int^{t_1}_{t_0}\|{\bf c}'(t)\|\,{\it dt}. \]

The integrand is the square root of the sum of the squares of the coordinate functions of \({\bf c}'(t)\): If \[ {\bf c}(t)=(x_1(t),x_2(t),\ldots,x_n(t)), \] then \[ L({\bf c})=\int^{t_1}_{t_0}{\sqrt{(x_1'(t))^2+(x_2'(t))^2 +\cdots +(x_n'(t))^2}}\,{\it dt}. \]

example 5

Find the length of the path \({\bf c}(t)=(\,\cos t,\,\sin t,\,\cos 2t,\sin 2t)\) in \({\mathbb R}^4\), defined on the interval from 0 to \(\pi\).

solution We have \({\bf c}'(t)=({-}{\sin t},\,\cos t,-2\,\sin 2t,2\,\cos 2t)\), and so \[ \|{\bf c}'(t)\|={\sqrt{\,\sin^2 t+\,\cos^2 t+4\,\sin^2 2t +4\,\cos^2 2t}}={\sqrt{1+4}}={\textstyle\sqrt{5}}, \] a constant, so the length of the path is \[ \int^\pi_0\sqrt{5}\,{\it dt}=\sqrt{5}\pi. \]

example 6

Consider the graph of a function of one variable \(y=f(x)\) for \(x\) in the interval [\(a, b\)]. We can consider it to be a curve parametrized by \(t = x\), namely, \({\bf c}(x)=(x, f(x))\) for \(x\) ranging from \(a\) to \(b\). The arc-length formula gives \[ L({\bf c})=\int^b_a \sqrt{1+[f'(x)]^2} \, {\it dx}, \] which agrees with the formula for the length of a graph from one-variable calculus.